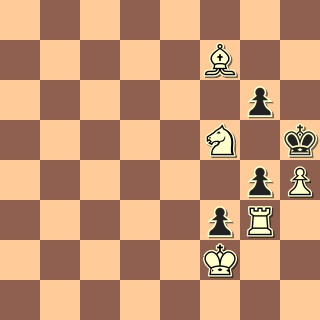
....heeft nog eens wat....
Nee, het zijn geen bijzonder waardevolle goederen, maar toch. Zo gaar ik ongeveer van alles op schaakgebied bij elkaar wat enige unieke uitstraling heeft. Een notatiebiljet uit een, hoe moet ik het zeggen, een stad die niet meer zo heet uit een land dat nog wel bestaat maar aldaar niet meer het land is. Nou ja.
Zo ongeveer. Een notatiebiljet uit 1929 van de Schachclub “Morphy” uit de tóen Duitse stad Breslau, thans de Poolse stad Wroclaw en een wedstrijd tussen
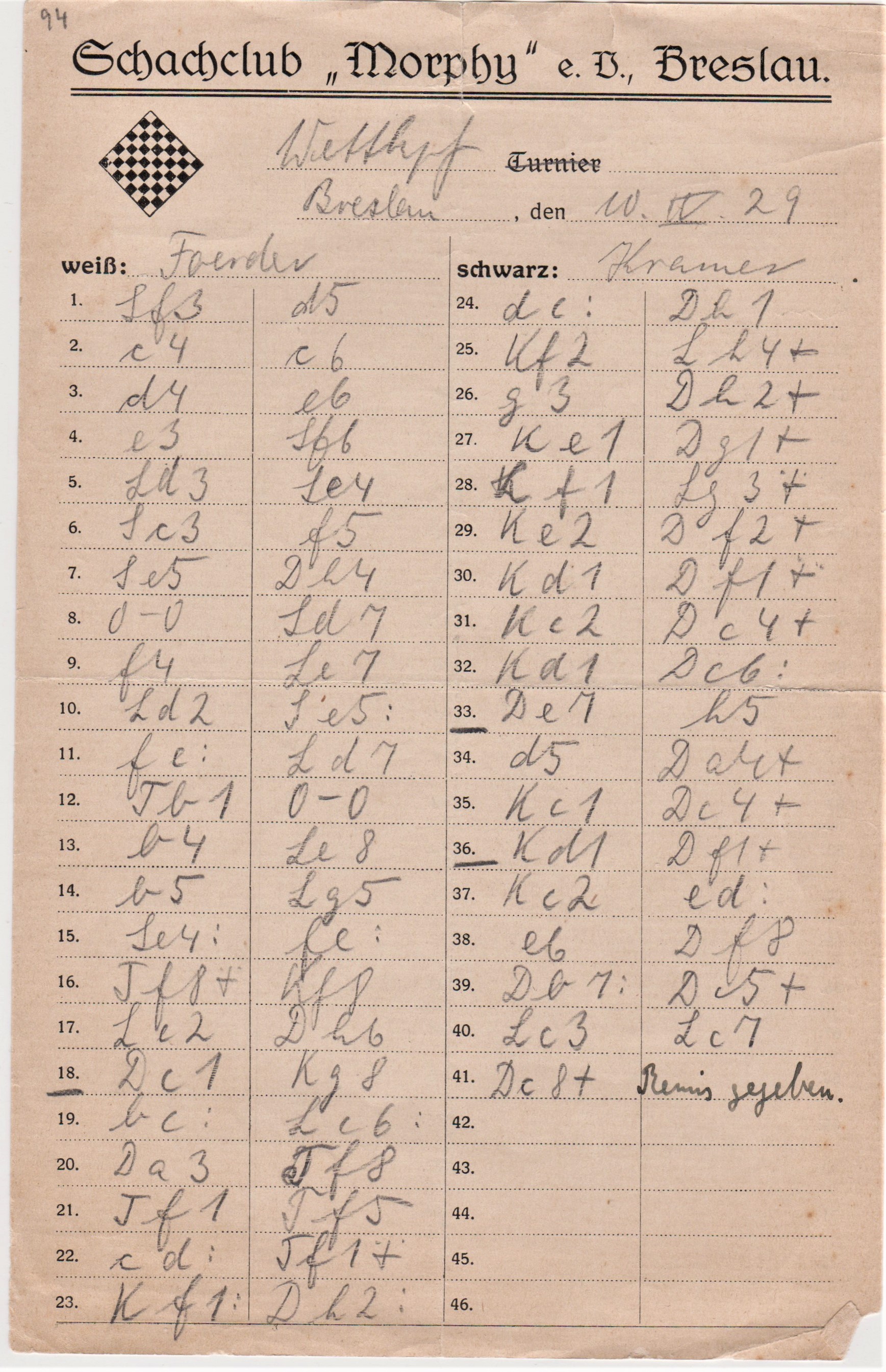
Heinz Foerder en ene Kramer. Wie die Kramer was, kon ik tot op heden niet achterhalen, maar Foerder, Heinz Foerder kennen we weer wel. Enkele jaren geleden schreef ik in Caïssanieuws dat deze schaker rond 1937 zijn naam veranderde in Josef Porath en kampioen van zowel het voormalige mandaatgebied Palestina is geweest én van het latere Israël.. Toch aardig om weer eens een ruim negentigjarige partij te bekijken van het origineel notatiebiljet.
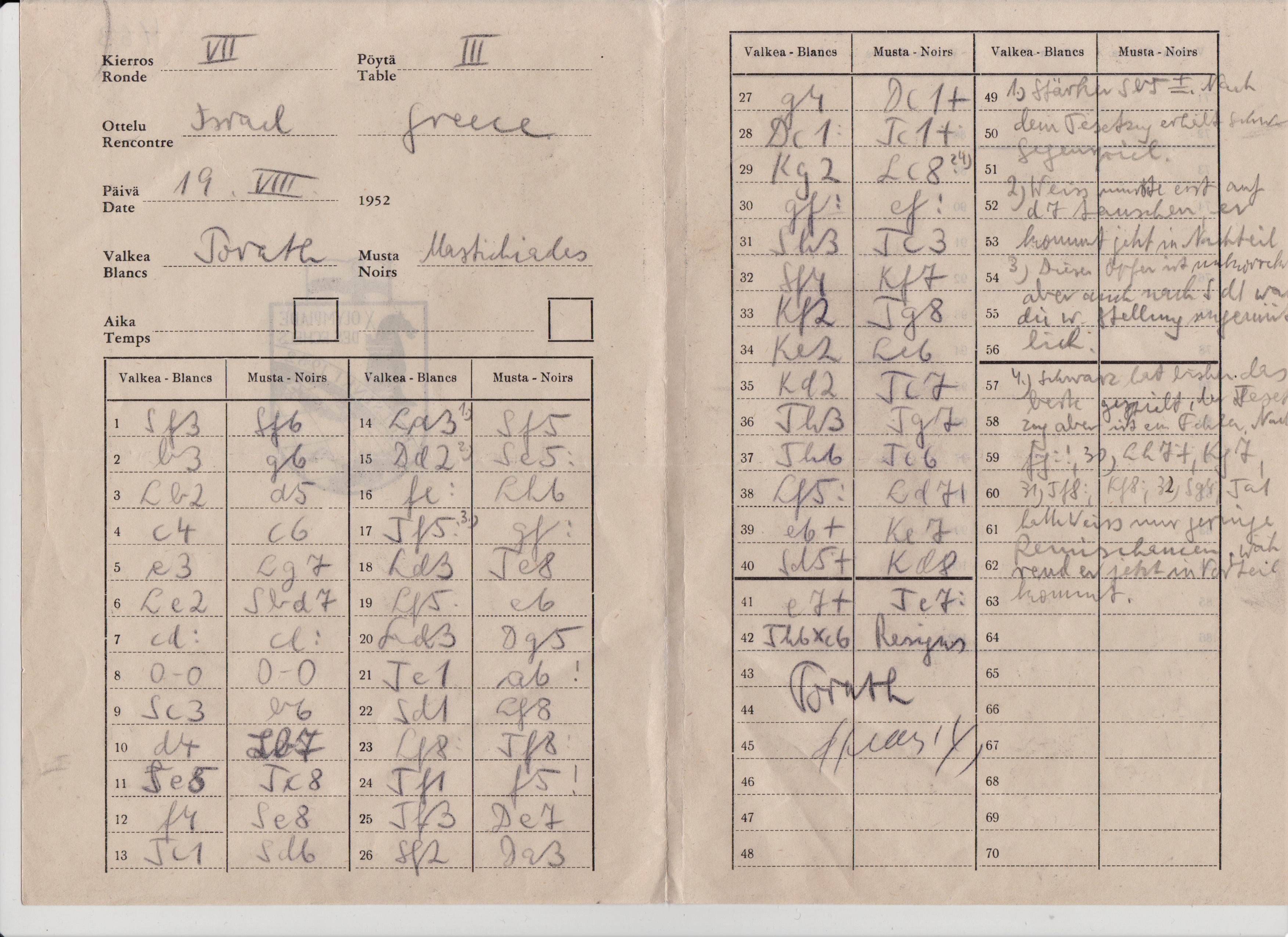
Zo onderschepte ik van dezelfde schaker een notatiebiljet uit mijn geboortejaar, 1952 en het bijzondere daarvan is dat het biljet altijd net zo oud is als dat ik zelf ben. De gedachte alleen al dat ik als kleine schreeuwerige baby lag te krijsen en tegelijkertijd iemand in Helsinki een partijtje schaak speelde…

Tja, en dan dat ene boekje, wie heeft dat nog in zijn bezit? Het boekje met het opschrift Eindelijk hoor…. Tien jaar Gambiet waar er, volgens de inhoud, 200 van zijn gedrukt en waarvan in ieder geval ik er één van heb bewaard.

Het “eindelijk 10 jaar…” intrigeert mij, want dat was in 1991, over een maand alweer dertig jaar geleden. Korte artikeltjes van Leon Pliester, Errit Petersma, Frans Oranje. Maar ook Theo Weijers en Robert van het Kaar….
…Um Mitternacht
Kämpft’ich die Slacht,
O Menschheit, deiner Leiden;
Nicht könnt’ich sie entscheiden
Mit meiner Macht
Um Mitternacht , zo begon Frans Oranje met een gedicht van Friedrich Rückert zijn artikel “het koffertje” en ik slik even wanneer ik de term de Cor-Haas-doorbraak lees…
En dan: tussen wat boeken een catalogus uit 1984, een heuse schaakpostzegelcatalogus. Volgens de op de voorkant geschreven podloodprijs heb ik daar een zeven gulden voor neergelegd. Ik snuffel even de inhoud door en die verteld mij dat in 1947 in Bulgarijë de eerste schaakpostzegel werd uitgegeven gevolgd door de Sovjet Unie in 1948 tijdens de vijfde wereldkampioenschappen gehouden te Moskou. En het was J.R. Capablanca (José Raul) die de eer te beurt viel om als eerste schaker op een postzegel te verschijnen, in 1951, een zegel uit Cuba tijdens of na 30 jaar WK schaken en de prijs, althans in 1984, voor de gehele ongestempelde serie van zeven zegels was bijna 100 gulden.

De eerste Nederlandse schaakpostzegel verscheen pas in 1973, elf jaar later dan de Nederlandse Antillen.
Aldus: ome Willem